Rocket Propulsion - Changing Momentum

To analyze this process let us consider a rocket being fired in upwards direction and we neglect the resistance offered by the air to the motion of the rocket and variation in the value of the acceleration due to gravity with height

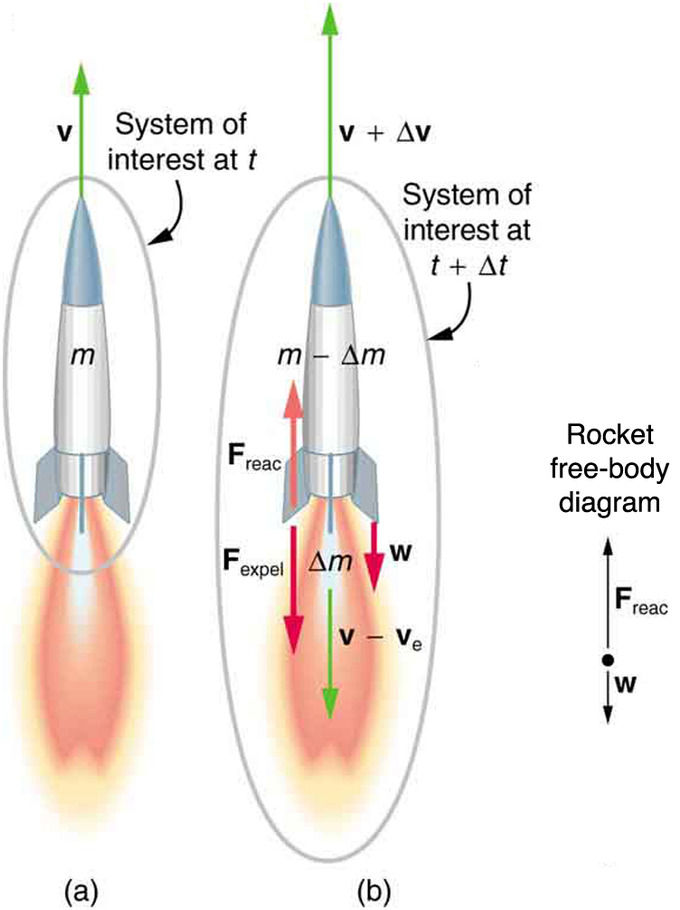
Figure above shows a rocket of mass m at a time t after its take off moving with velocity v. Thus at time t momentum of the rocket is equal to mv. Thus pi=mv

• Now after a short interval of time dt gas of total mass dm is ejected from the rocket

• If vg represents the downward speed of the gas relative to the rocket then velocity of the gas relative to earth is vge=v-vg And its momentum equal to dmvge=dm(v-vg)

• At time t+dt, the rocket and unburned fuel has mass (m-dm) and its moves with the speed v+dv. Thus momentum of the rocket is =(m-dm)(v+dv).

• Total momentum of the system at time t+dt is pf=dm(v-vg)+(m-dm)(v+dv) Here system constitute the ejected gas and rocket at the time (t+dt)

• From Impulse momentum relation we know that change in momentum of the system is equal to the product of the resultant external force acting on the system and the time interval during which the force acts

• Here external force on the rocket is weight -mg of the rocket ( the upward direction is taken as positive)

• Now, Impulse =change in momentum

Fext.dt=pf-pi or -mgdt=dm(v-vg)+(m-dm)(v+dv) – mv

or -mgdt=mdv-vgdm-dmdv ( term dmdv can be dropped as this product is negligible in comparison of other two terms.